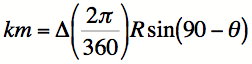
GLG410--Computers in Earth and Space Exploration

Announcements Syllabus Schedule Weekly lecture notes Assignments Links

Matlab Introduction

Matlab is a program that has been developed for the general solution of mathematical equations, data processing, and data display. MATLAB is an acronym for MATrix LABoratory and it is a highly optimized numerical computation and matrix manipulation package. It is an excellent tool for developing numerical models of problems, performing mathematical operations on large data sets, displaying data in one, two, three, or four dimensions, and solving simultaneous equations. In general, Matlab has been developed as a numerical tool and so best works on real numbers, rather than symbolic operations.

Matlab is a product of The Mathworks. Cleve Moler is the inventor of Matlab and a founder of Matlab.

In short, if you can write an equation that you think represents a relationship between two or more variables and need to graph your results, Matlab is the tool to use. First, we will go through a short introduction on Matlab concepts, entry formats, graphics, M-files, and functions.

Getting started

Copy and paste this into the Matlab command line: playbackdemo('GettingStartedwithMATLAB', 'toolbox/matlab/demos/html')

Startup Matlab Through "My Apps"

Matlab startup instructions (slightly old, but still basically works). Any of the various versions of Matlab will work for our purposes. You will want to "Run app now."

Video demonstration:


Matlab GUI Overview





Each version of Matlab (Mac/Windows/Linux) has a similar layout. There are only 3 elements in this window I use on a regular basis:

Basic Math Functions (Matlab as a fancy calculator)

Matlab can be used to perform the very simplest of calculations. Functions used to do basic math are quite intuitive and so I won't dwell on this topic for long. But these functions do form the basis for all of your problems that you will solve within the Matlab environment.
NOTE: For multiplication, division, and exponents, remember to use the dot (.) BEFORE the math symbol. This is not necessarily needed all the time, but is good practice to use it anyway to avoid problems with vector and matrix operations in the future.
Addition (+) 
>> 4 + 7

ans =

    11
Subtraction (-) 
>> 48 - 8.2

ans =

    39.8
Multiplication (.*) 
>> 4.53 .* 6

ans =

    27.18
Division (./) 
>> 200 ./ 50

ans =

    4
Exponents (.^) 
>> 4.1 .^ 3

ans =

    68.921
Trig Functions in Radians (sin, cos, tan, sec, cot, csc) 
>> sin(0.8)

ans =

    0.71736
Trig Function in Degrees (sind, cosd, tand, secd, cotd, cscd) 
>> sind(90)

ans =

    1
Inverse Trig Functions in Radians (asin, acos, atan, atan2, asec, acot, acsc) 
>> acos(0.567)

ans =

    0.96794
Inverse Trig Functions in Degrees (asind, acosd, atand, asecd, acotd, acscd) 
>> acosd(0.5)

ans =

    60
Square Roots 
>> sqrt(16)

ans =

    4
Exponentials 
>> exp(2.3)

ans =

    9.9742
Natural Logarithms 
>> log(456384)

ans =

    13.031
Base 10 Logarithms (this is special) 
>> log10(10000)

ans =

    4
Absolute Value 
>> abs(-31.45)

ans =

    31.45
There are a few special numbers that are important to know. Some you will use all the time, some not so much.

Pi 
>> pi

ans =

    3.1416
Imaginary (Complex) Numbers 
>> i

ans =

    0 +    1i
Not-a-Number (this acts like a place holder for a value, except it has no value) 
>> NaN

ans =

    NaN
Infinity 
>> inf

ans =

    Inf
Smallest incremental number (the precision of the computer) 
>> eps

ans =

    2.2204e-16
Combining operations - using parenthesis ()
The next thing we need to do is start combining these operations within one line. 
>> 2 .* pi ./ 360 .* 6371 .* sind(90 - 43.8)

ans =

    80.256
REMEMBER YOUR "ORDER OF OPERATIONS"!! I recommend using parenthesis for EVERY separate operation to organize your equations. A common source of error is either forgetting to close parenthesis (easily corrected), or putting parenthesis in the wrong place (hard to find and correct!).
Here is how I would re-type the above equation:
>> (2 .* pi ./ 360 .* 6371 .* sind(90 - 43.8)

??? (2 .* pi ./ 360 .* 6371 .* sind(90 - 43.8)
                |
Error: Expression or statement is incorrect--possibly unbalanced (, {, or [.
Oops! I forgot to close a parenthesis. Let's try it again.

If you type in a complex expression and make an error, you can edit the previous expression by pressing the Up arrow on your keyboard to recall the last line. Press the Up Arrow or Down Arrow several times to recall other recent command lines. Use the Left and Right Arrow to move through the command and insert numbers or text or you may also delete something. 
>> ((2 .* pi) ./ 360) .* (6371 .* sind(90 - 43.8))

ans =

    80.256
This time I grouped the parts of the equation that make sense. For full disclosure, this particular equation is for converting degrees of Longitude to kilometers around a given line of Latitude.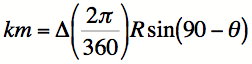

Variables

All answers up to this point have been output by Matlab as: 

ans =

    80.256
Matlab is assigning your answer to a default variable called ans. Everytime you do a calculation in Matlab, ans is replaced in the Workspace window.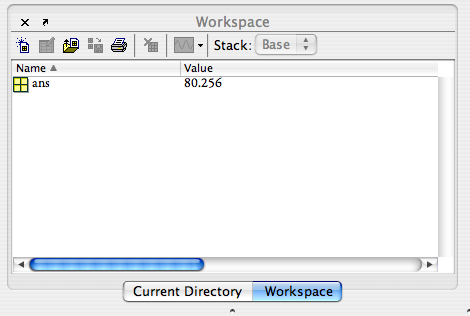

Variables allow you to store information within the Matlab environment to use it at a later time. Here is how you can assign something to a variable: 
>> kilometers = ((2 .* pi) ./ 360) .* (6371 .* sind(90 - 43.8))
You will notice that Matlab has been echoing your output by saying: 
kilometers =

    80.256
Now we can use this variable in another equation. Lets just say we want to convert the kilometers to miles. 
>> miles = kilometers .* 0.62137

miles =

    49.869
SEMICOLONS
If you do not wish to see a confirmation of your assignment, include a semicolon after the operation. This rule holds for all assignments or operations-- if you do not want to see the result of the operation, but simply wish to store it in another variable, use a semicolon: 
>> kilometers = ((2 .* pi) ./ 360) .* (6371 .* sind(90 - 43.8));
Naming Conventions/Suggests (Any Programming Language)

Scalars, Vectors, Matrices (Arrays)

An advantage of Matlab is its ability to handle vectors and matrices in an intuitive way. Until now, we have dealt only with scalars. You can create vectors and matrices and assign them to variables. Here is how:

Row Vector 
>> RowVector = [1 2 3 4 5 6 7 8 9 10];
>> RowVector

RowVector =

    1 2 3 4 5 6 7 8 9 10
Column Vector 
>> ColumnVector = [1; 2; 3; 4; 5; 6; 7; 8; 9; 10];
>> ColumnVector

ColumnVector =

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
Matrix (2 x 5) 
>> Matrix = [1 2; 3 4; 5 6; 7 8; 9 10];
>> Matrix

Matrix =

    1  2
    3  4
    5  6
    7  8
    9  10
Array Operations 
>> Matrix = Matrix .* 2;
>> Matrix

Matrix =

    2  4
    6  8
    10  12
    14  16
    18  20

Video demonstration of simple matrix math:


Video demonstration of how to build a vector with elements separated by a constant increment:

Array Indexing (any kind of vector - 1 row or 1 column) 
>> RowVector(3)

ans =

    3

>> ColumnVector(4)

ans =

    4
Array Indexing (matrices) 
>> Matrix(3,2)

ans =

    6
NOTE: Rows are referenced first, then columns.
Array Indexing (entire row or column) 
>> Matrix(3,:)

ans =

    5  6
Rules to Remeber

Text and Character Arrays

You can assign text to a variable as well as numeric data. Each character, including white space, occupies one place in the character array (it is like a vector). Use single quotes, ' to denote text.
>> Name = 'My name is Kevin';
>> Name

Name =

My name is Kevin
This is a 16-element array.

Bringing Data Into Matlab

Lets introduce this concept by using real data. Here is daily water discharge (cubic feet per second) for the Salt River at Priest Dr. near Phoenix, AZ for all of 2008.
  1. Save the file from the browser to the local hard disk as "SRDischarge.txt".
  2. Create a directory on MyFiles called "glg410_matlab".
  3. Move file from local hard disk to this directory on the MyFiles.

Video demonstration:


Loading Text Files 
>> load('SRDischarge2008.txt','-ascii');
The first argument in the load function is the filename. The second argument is the file type. In the case of a text file, it is always '-ascii'.

The file has 2 columns of data. It loads into Matlab as a 366 x 2 matrix with the name of the file as the new variable name. (NOTE: This only works if the text file has ONLY numeric data! No headers.)
Column 1: days of the year (1-366 for 2008)
Column 2: discharge (cubic feet per second)

Basic Statistics and Information Gathering

We can easily find out some statistical information on our data matrix, such as the minimum and maximum values, average value, etc. Here are some examples:
Minimum Value (2nd column - discharge) 
>> min(SRDischarge2008(:,2))

ans =

    0
Maximum Value (2nd column - discharge) 
>> max(SRDischarge2008(:,2))

ans =

    5900
Average or Mean Value (2nd column - discharge) 
>> mean(SRDischarge2008(:,2))

ans =

    5900

Basic Plotting Functions

The next thing we need to be able to do is plot the information in a graph. The most basic function you will use is the plot command. Lets see what this does:
>> plot(SRDischarge2008(:,1),SRDischarge2008(:,2));
The first argument is the x-axis values. The second argument is the y-axis values. (NOTE: These MUST BE the same length!)

This plot isn't very interesting though. (1) There is no title, so you don't know what information it is trying to convey. (2) The axes are not labeled, so you have no idea what the numbers are telling you. (3) Points are connected by a line. Is this the best way to show the data?

A few more useful commands AFTER you have plotted your data can really give the graph a boost. Here are some examples:
Plot Title 
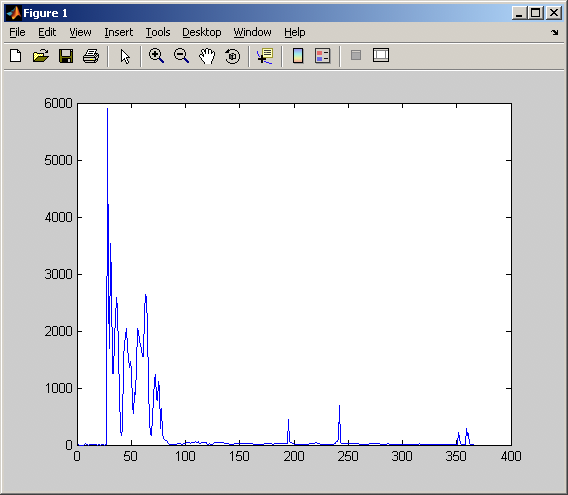
>> title('Salt River Discharge at Priest Dr. - 2008');
X-Axis Label 
>> xlabel('Day of Year');
Y-Axis Label 
>> ylabel('Daily Discharge (cfs)');
Now what do we have.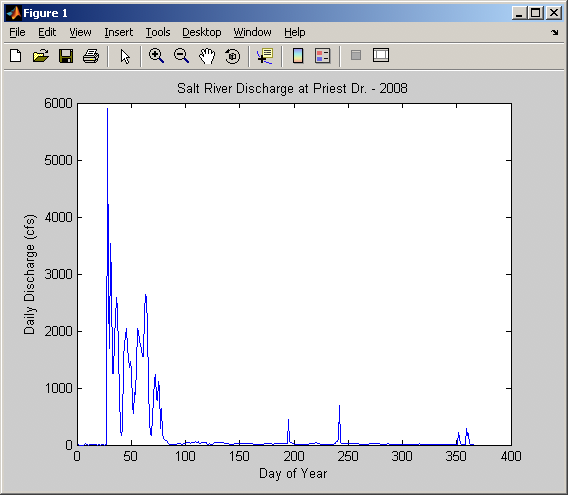

NOTE: You can also play around with the plot using buttons and functions within the Figure Window.
Saving a graph to a JPEG is very helpful for placing this graph in the context of a report (or maybe your homework). To save a figure, you will use the print function. Here is how to do it:
>> print('discharge.jpg','-djpeg');
The first argument is the filename of the JPEG image. The second argument ('-djpeg') tells Matlab that you are saving it in JPEG format.

Saving and Loading Workspace

You will eventually want to save the work that you have done in Matlab. You can save an entire Workspace into a MAT-file (which is just a binary file that is formatted especially for the use of Matlab). You do this by using the save function. 
>> save
The default filename for your saved workspace is "matlab.mat". If you want to save it under a different name, you add that name as an argument to the function. 
>> save('lecture3.mat');
NOTE: This will ONLY save the variables in your workspace. It DOES NOT save figures or plots that you have made.
To load in a saved MAT-file, you will use the load function, similar to what we did with the text files. 
>> load('lecture3.mat','-mat');
The first argument in the filename. The second argument is the format of the file you are wanting to load. For MAT-files, this is always '-mat'. (NOTE: In this case, the second argument is optional because '-mat' is the default choice.)

GLG410/598 Computers in Earth and Space Exploration
Last modified: September 22, 2011