Lecture 5: Basic statistics in a spreadsheet: histograms, frequency, skewness

Example: Pebbles on a Beach

Let's take an example of the masses of pebbles on a beach. If you pick up a pebble on the beach, it is a specimen. It might not be representative of all the pebbles on the beach (population). But we cannot examine all of the pebbles on the beach, so we select a subset (10 or 100 or 1000, etc.) and that is a sample (dataset) of the population which we hope is representative. Here we will play with a small data set of pebbles. Open this web page in a browser:

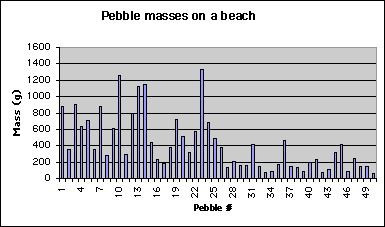
Below I show a plot of the masses of the individual pebbles in our sample: (a default Excel plot). This chart was made with the Chart Wizard, choosing columns and adding labels, and gives a visual impression of the data, but can we do more? Of course!

Sorting

The simplest way to look at a dataset is just to sort it. In Excel, look at Data->Sort. You can sort on multiple columns (size, then shape, etc. if they are in your spreadsheet). One really important point is that you should be aware that sorting with only one column will scramble your data. So, you should probably select all of the columns and then in the sort dialogue, choose the column(s) on which you want to sort.

Introduction

In today's lecture we are continuing our introduction to Microsoft's Excel. We will cover some basic statistics in Excel: histograms and frequency. If your data set is either huge or complicated looking, what is the best approach for analyzing it? Here are some options:

1. Discard all the data that do not fit some preconceived notion or model. For some data sets, this might mean throwing away most of the data! This is very definitely not recommended although it is quite frequently done.
2. Plot the data in a way that allows the general properties of the data to be visualized.
3. Perform statistical (or other scientific) analyses. In other words, examine all the characteristics of the data.

Obviously, we should pursue options 2 and 3. We can apply some statistical tools to Earth and Space science problems. We should be careful however, that a statistical description of our data does not bias our view of the data. So... What is a statistic? --> An (estimated) parameter that characterizes a dataset. Wikipedia.org states:

Statistics is a mathematical science pertaining to the collection, analysis, interpretation, and presentation of data. It is applicable to a wide variety of academic disciplines, from the physical and social sciences to the humanities; it is also used for making informed decisions in all areas of business and government.

Statistical methods can be used to summarize or describe a collection of data; this is called descriptive statistics. In addition, patterns in the data may be modeled in a way that accounts for randomness and uncertainty in the observations, to draw inferences about the process or population being studied; this is called inferential statistics. Both descriptive and inferential statistics can be considered part of applied statistics. There is also a discipline of mathematical statistics, which is concerned with the theoretical basis of the subject.

The word statistics is also the plural of statistic (singular), which refers to the result of applying a statistical algorithm to a set of data. Thus we speak of employment statistics, accident statistics, etc.

When we work with with a large number of observations, it is desirable to be able to describe some of the basic characteristics of the data with single numbers that describe some essential feature of the data, specifically the distribution of numbers. Some important examples are:

• location of the distribution, which characterizes some central point of the "mass" of the distribution (this is commonly referred to as the mean or average)
• dispersion of the mass of the mass about this central value, or a measure of "spread" (you've more likely heard of this as standard deviation)
• skewness of the distribution, which characterizes the asymmetry of the distribution about the central point.

Measures of location

Here are some basic representations of the mass of the distribution that we'll quickly play with:

Measures of dispersion

Frequency histograms

How can we improve on the pebbles chart and possibly display the distribution of pebble masses graphically? The simplest method uses the frequency histogram which allows the general properties of the distribution to be visualized. If you haven't already done it, install the Analysis Tool Pack [choose Tools>Add Ins.., then check both Analysis Tools Pack boxes], then go to the Tools/Data Anaysis... dialog box, scroll down and choose Histogram.

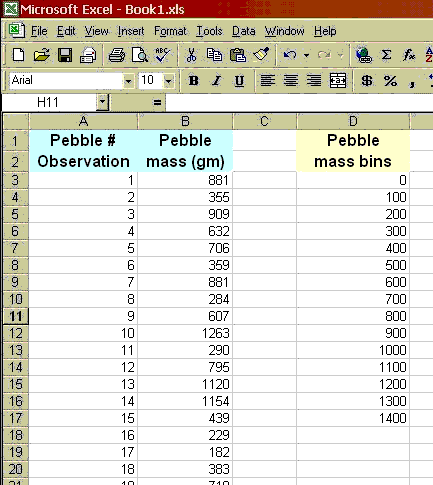
To construct such a plot, we need to decide on specified ranges of values (bins) within which we want to count the number of pebble masses (Frequency distribution). For example, you might bin masses from 0-100, 100-200, etc. Go ahead and make a column with values 0, 100, then drag the lower right box corner down, which will fill lower cells with that pattern; stop when an appropriate range has been created. Then when we plot the frequency distribution using a bar chart, we have a frequency histogram. Note we might also look at the cumulative frequency distribution in which we add the cumulative percentage of the total specimens that are in each bin. The curvature of the cumulative distribution plot tells us something about the dispersion of the dataset.

Here I will walk you through making this first histogram with a frequency curve, for the pebble data set. You very well may do this dozens of times this semester, so become familiar with these steps. For this example, I'm assuming you already have your pebbles data set correctly entered into a spreadsheet.

1. First, you need to decide on your bin width and range. A bin is the numeric range for which any given bar of the histogram chart adds up. For our pebbles histogram, I think bin ranges of 0-100, 100-200, etc., are appropriate. Make as many bins as you need to completely contain your data. Mine looks like this: (Note: I made labels and shaded labels by right clicking, and choosing Format cells, then click the Patterns tab).



2. Now launch the Histogram tool: go to Tools>Data Analysis..., and choose Histogram from the list of tools. You'll see the dialog box wants info about an Input Range ("1" in the diagram below) and a Bin Range (2, below). Click the highlighted square for input range, then click-drag on the spread sheet to encircle your pebble masses.
   
   You will notice the input window as you do the click-dragging. Then click the button on the right of this window:
   
   
   Then do the same for Bin Range. Finally, click the Cumulative Percentage and Chart Output options (see "3" in the image on the last page), then OK.
3. You are thrown into a new sheet that should show the following bin, frequency, and cumulative % information:
   
   
   The chart is to the right of this, and probably looks something like this:
   
   
   Last but not least... we must clean up all of the chart junk, and make this chart more palatable.
   After clean up, a plot combining the Frequency histogram with the Cumulative Frequency, using 100 g bins for the histogram looks like:
   
   

   Skewness

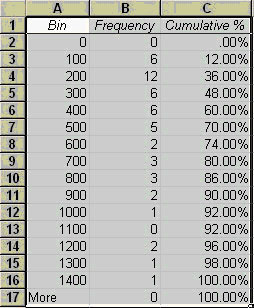
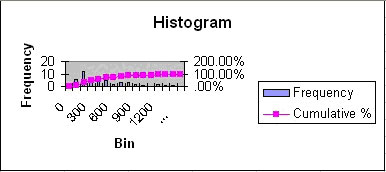
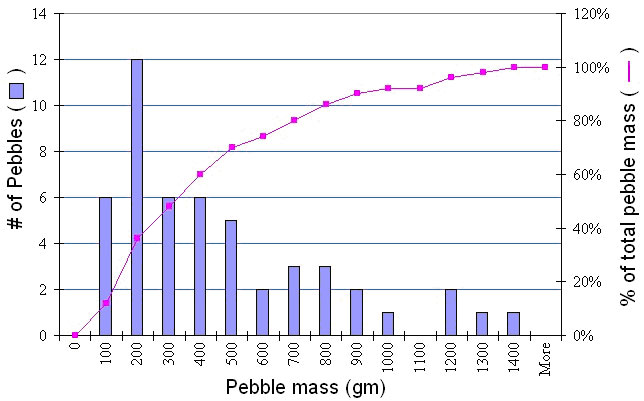
   Note that the mean is not near the center of the data. These data have significant positive skewness. Positive skewness means that the tail of the distribution is longer to the right. Negative skewness is the opposite. In general, a bigger number means more asymmetry. (be careful that you know what the program is actually computing). Standard skewness is in units of the standard deviation, so if it is <1, then we are close to being symmetric. The skewness is based on the deviations cubed:

   
   Compute the skewness of the pebble distribution:
   
   =SKEW( )
   
   I get a skew of 1.17 which is closer to symmetric than I expected!
   

   Earthquake catalog example and assignment

   The Advanced National Seismic System managed by the maintains an authoritative earthquake catalog of global events since 1898:
   
   http://www.ncedc.org/anss/catalog-search.html
   
   Here is an image that will remind you of how to fill out the search window: explanatory graphic.
   
   Choose any region in the world of interest. Use an atlas or Google Earth to help you figure out the latitude and longitude of the area of your interest. I encourage you to work near plate boundaries, especially subduction zones). Here is a series of maps that might help you: USGS World Seismicity Maps. Keep the size of the area to less than about 10 degrees on a side, or you will get too many earthquakes (note that Excel can only handle 64,000 rows!).
   
   
   

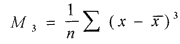
   Tasks	Hints and help
   Copy the data with the headings into Excel	Be careful that you keep the number of events smaller by trial and error. Make the start date more recent or the area smaller. On a slow machine, it can take a long time to copy from the browser and paste. Once you have pasted it into Excel, then parse using the Data->Text to columns command with Fixed Width.
   Produce a histogram of depth	See above in the lecture for how to do it. Remember you need to define your input bins. They should go from the minumum depth to the maximum depth (compute these) in a regular way (10 or 50 or 100 km bins).
   Compute mean depth, standard deviation of depth, and skewness of depth	See above lecture
   Sort by increasing depth. Make an xy map of the dots, but with the dots colored by depth (don't worry if there are none at certain depths): 0 to 35 km orange 35 to 70 km yellow 70 to 150 km green 150 to 300 km blue 300 to 500 km purple 500 to 800 km red Use a different set of ranges for the colors if your events don't go so deep.	Here is a graphic for how the sorting might look: sort.jpg. This graphic shows importantly how to work with the source data in the Chart: Click on the Chart, and the go to Chart menu->Source data: plotbydepth.gif. I have labeled the key features. Make sure you choose the right series (if there is more than one) on the lower left. Then switch the X and Y values by manually editing to which columns they point. Also, give it a name while you are here so the explanation (legend) will be correct. This graphic shows how to color the dots: colordots.jpg. Remember to just double click on one of the dots of the series you want to change. This graphic shows how to add another series: addevents.jpg. Select the group of latitude longitude pairs from the spreadsheet and copy them. Then go to the chart, click on it once and then File->Paste Special. Make sure you have selected New Series and Categories (X Values) in First Column (see addevents.jpg). My final map looks like: finalcolormap.jpg
   What do the depth statistics and your plot of the earthquake depths and positions tell you about what is happening in terms of seismic deformation in your study area?	Think about what you know about the tectonics of the study area. Recall also that the temperature of transition from brittle to ductile behavior is about 300 C.
   Plot magnitude versus day. Do you see any long term trends? Are earthquakes on the increase?	Just plot the date versus the magnitude column. One issue here is getting the axes labels right. Remember to double click on the axis (X axis) to change it from the defaults. While the dates are nicely formatted on the chart, they are just numbered in days since 1900 in the chart editor. So, figure out how many days are the earliest and latest events in your study and use them to define the axes. Also, make sure the magnitudes (Y axis) range is sufficiently narrow so it spans the data only. This graphic shows a bit about the axis editing: timelabels.jpg. This graphic shows the final result in my example: finaltime.jpg.
   Produce a histogram of magnitude with 0.1 unit bins. What is the minimum and maximum? What is the most common magnitude? Why do you think the minimum is where it is? What about the maximum?	Remember that the earthquake magnitude bins should only really go from your minimum (or slightly less) to your maximum (or slightly more). Or, you can go from magnitude 0 to magnitude 9, but no earthquakes will be beyond that range. Follow the instructions about histogram making from above in the lecture.
   It is unlikely that your earthquakes will have any interesting depth pattern north-south or east-west. If we rotate the data by enough so that you can plot a cross section through it (rotated latitude versus depth), you can then use one of the axes directions as your X axis (distance in degrees along the cross-section) versus depth. Choose an interesting direction based on what you know about the tectonics and geology of the area. It is obvious what the direction would be for a subduction zone: down the subduction zone. The result will be a cross section through the data projected to a vertical plane. What does the cross section show in terms of seismicity distribution and tectonic processes?	Use the equations we introduced in the Rotation and translation exercise. Recall that the rotation equations rotate about the 0,0 axis. So, first we need to translate the data to get it close to 0,0. Then we rotate it. Set up some new spreadsheet columns to the right of your data: Mean lat = average latitude of the entire data set Mean long = average longitude of the entire data set Displaced long (E) = subtract the mean longitude from each of the longitude values. Put this column first relative to the Displaced lat so it will be easier to plot later Displaced lat (N) = subtract the mean latitude from each of the latitude values. Plot those two columns in an XY chart. Rotated Lon (E') = Use the rotation equations from the Rotation and translation exercise for E'. You will need a phi value converted from degrees to radians Rotated Lat (N') = Use the rotation equations from the Rotation and translation exercise for N'. Plot the Rotated Lon and Rotated Lat on top of the Displaced Lon and Displaced Lat. As you change phi, you should see the rotated data rotate. Rotate until the longitude (E-W) is along the direction that you think is the appropriate cross section Negative depth = multiply the depth by minus one so that it will be negative going down into the earth and thus plot correctly. Plot the Rotated Lon (your distance along the profile) on the X axis versus the negative depth to make the cross section. This graphic shows how I set up my spreadsheet: rotandtransspreadsheet.jpg This graphic shows how my final charts look: finaldepthxsec.jpg If either of those graphics look blurry in your browser, click on them or make then full size. They ar bigger images.

   
   This assignment is due by 5 pm, October 1 as a link on your assignments web page. Make sure that all of your plots do their best to obey the rules of graphical excellence as advocated by Tufte (Data Visualization Lecture). Note that my examples above do not follow such excellence. I expect that yours will be better. Also, make sure that the spreadsheet is well organized and formatted.
   
   

   ---

   Some of the pebbles example comes from short course notes, Statistical inference for Geology and Planetary Geology, L. S. Glaze and S. M. Baloga, 1997; and also: Waltham, D., 1994, Mathematics: a simple tool for geologists, New York: Chapman and Hall, 189 p.

   Web page originally by Prof. Ramón Arrowsmith with major modifications and additions from Prof. Ed Garnero and Prof. Steve Semken
   

   GLG410/598 Computers in Geology

   ---

   Last modified: September 27, 2007