GLG410--Computers in Geology

Announcements Syllabus Schedule Weekly lecture notes Links

Lecture 8: Exploring diffusion using Excel

Introduction

The rate of much natural phenomena goes with the gradient of a variable such as chemical diffusion (concentration), heat conduction (temperature), and slope dependent sediment transport (elevation). These relationships can be characterized by simple differential equations. In this lecture and exercise, we will work to show a simple numerical (approximate solution) to the diffusion erosion problem. Much literature in physics, engineering, math, and geoscience is dedicated to these problems. I reviewed the very basics in an appendix to my dissertation. THis is a useful reference to the content in the lecture Documentation (Arrowsmith, 1995).

Slope dependent sediment flux (transport rule)

A very simple rule for sediment transport is that the movement rate of material (sediment flux, qs) goes with the local slope (delta elevation over delta distance). We will assume that we are examining a profile of a hillslope over which this is the only way materials move. Soil creep, biogenic processes (burrowing, other animal induced disturbances), rainsplash, meteorite impact, etc. are processes which might drive sediment flux this way.

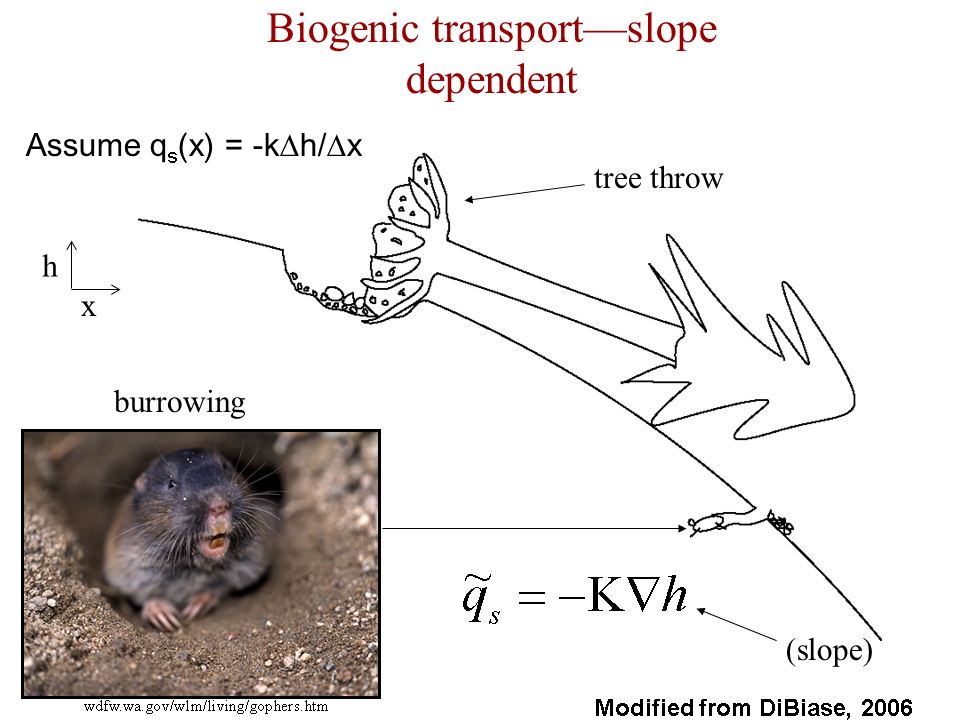
Basic idea of slope dependent sediment transport emphasizing biogenic driver (Dibiase, 2006)

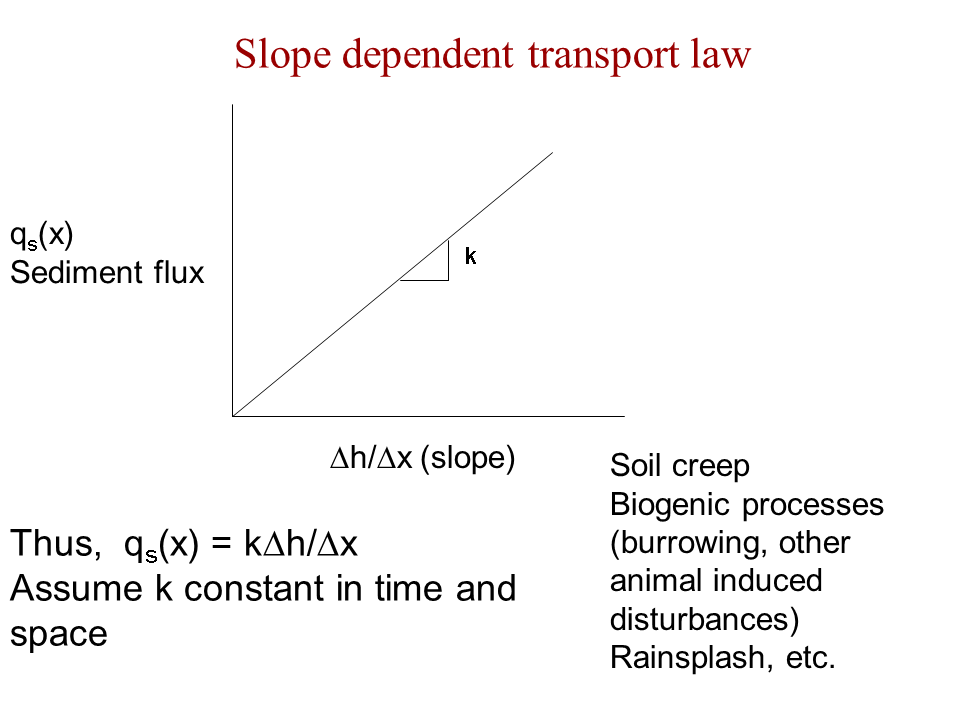
Slope dependent sediment transport. k is the rate constant.

Continuity

If we take our hillslope and divide it into small pieces, we can treat each like a little bank. The balance that is in each bank is the difference between what goes in (qs in) and what goes out (qs out). Δqs is simply then the difference between them. And, the change in sediment transport (Δqs) over that very small element (Δx) determines the change in elevation with time Δh / Δx This video tries to explain simply:

Pulling it together

Given the slope dependent transport rule and continuity, we can substitute -kΔh / Δx for Δqs:


Erosion rule

Numerical approximations for diffusion and set up in Excel

Quick review on gradients and indices

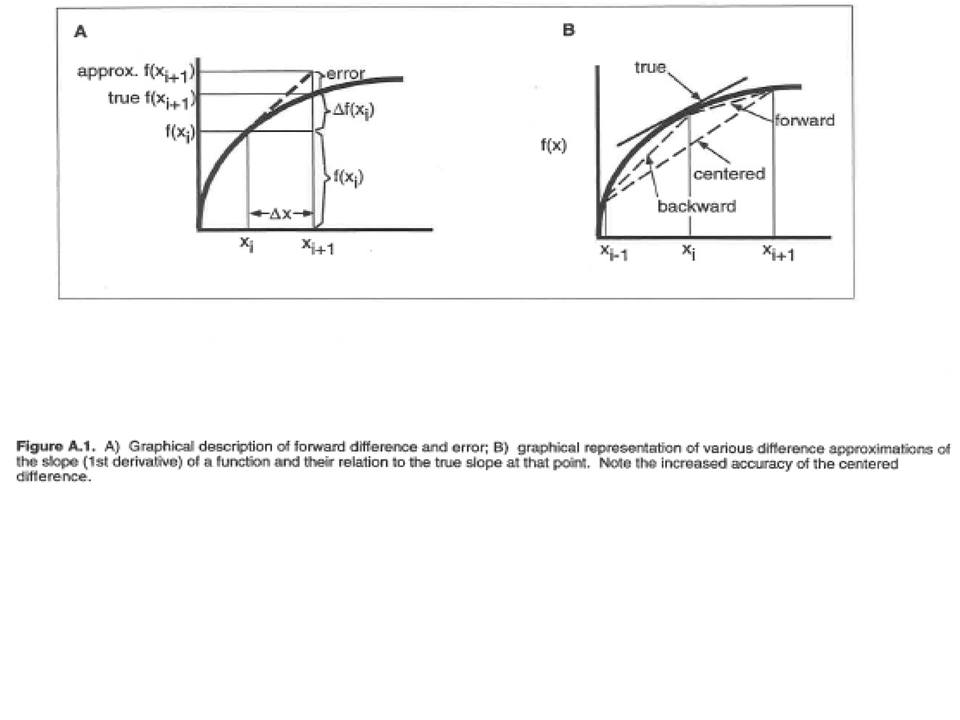
Before we get started on approximating the diffusion equation, let's remind ourselves about gradients ("slopes"). In the figure below, the left side shows a curve in black which we are trying to approximate. This can be done at any place along the curve. Our first location is at xi (i is called the index) and then we go a short distance Δx to xi+1. If we use just a linear extrapolation, the error is not too bad. On the right side of the figure, we add in a position at xi-1. Now we can try to approximate going forward or backward from xi. Or, more interestingly, we can go from xi-1 to xi+1 and then center at xi, but having gone a distance of 2Δx.

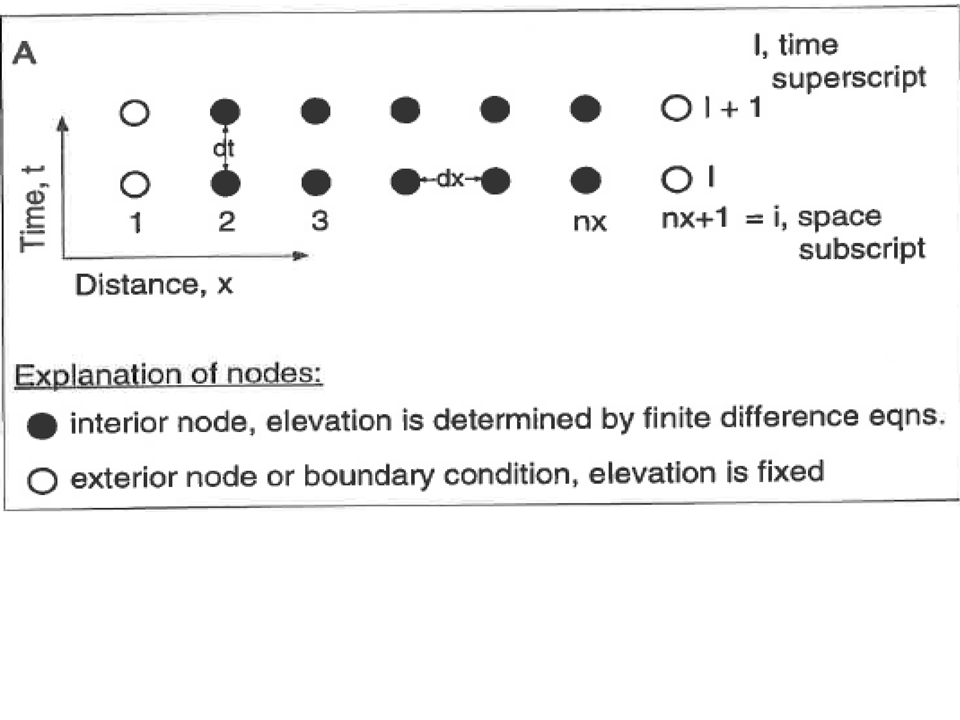
Basic difference equations for implementation

We set up the basic equations on "nodes"--these will ultimately be cells in our Excel spreadsheet). We treat time just as another coordinate (index is l) and march forward, estimating the future elevation as a forward difference from now and we estimate the slope for our transport rate using a centered difference (index is i).



Narration of equations

Calculation nodes

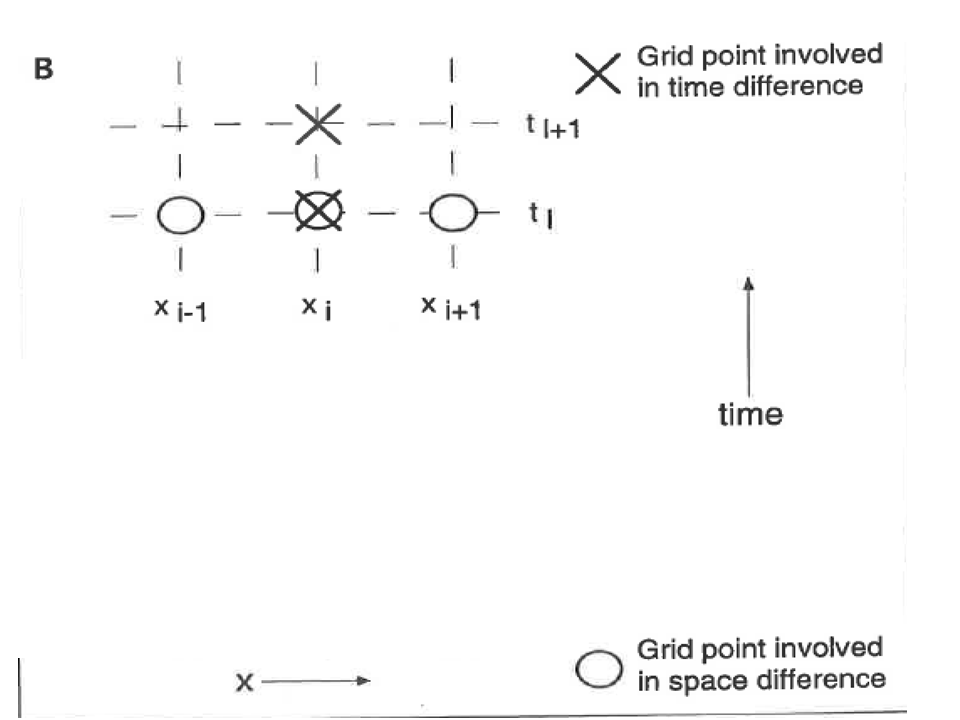
Calculation nodes detail

Excel implementation

Put it all together in Excel. Don't forget to keep it clean following Tufte's inspiration:

Background presentation including analytical solutions

Here is a ppt and pdf that includes the graphics from above as well as a couple of analytical solutions (exact integrations for set initial and boundary conditions) for the diffusion equation.

Assignment

  1. Implement the finite difference model for diffusion erosion in a spreadsheet. You should use one tab that is easy to read and interact with ("Interface") and then use a second tab that does all of the calculations ("Model Calculations"). You should have a chart that shows the initial and final forms and is not full of chart junk. Your model should have at least 30 space steps and at least 200 time steps.
  2. Using an idealized ramp-step initial form (what we have been demonstrating), make plots showing the initial form and final forms for:
    1. age = 1 ka, and k = 1 m2/kyr
    2. age = 5 ka, and k = 1 m2/kyr
    3. age = 10 ka, and k = 1 m2/kyr
    4. age = 1 ka, and k = 10 m2/kyr.
    Note that age and t are interchangeable here.
    Discuss the effects of varying age and k on the final form. HINT: look at the product age * t.
  3. Try different initial profiles. What are some other forms that might be interesting to see what happens as they change shape? Change the bold numbers in the Initial Elevations column and show the development over time of TWO different initial profiles of your choice. Show the profiles at time zero, an intermediate age, and a fairly old and well degraded age. What is the overall character of the change with time? Where does deposition occur and where does erosion occur? Indicate these zones on your plots. As the form ages, how well can you tell what the initial form was?
This assignment is due by the beginning of class, October 5 as a link on your assignments web page. Make sure that your spreadsheet is well organized, formatted, and annotated.

GLG410 Computers in Geology
Last modified: September 29, 2015